从拥挤的兔子到伪随机数算法

阅读 《复杂》 一书时的笔记及延伸。 本文涉及到的生态学、数学、计算机科学部分都比较肤浅，如有错漏，欢迎斧正。

又是兔子

我们多少接触过这样一个 问题：

1. 第一个月初有一对刚诞生的兔子
2. 第二个月之后（第三个月初）它们可以生育
3. 每月每对可生育的兔子会诞生下一对新兔子
4. 兔子永不死去

问：第 n 月时，一共有多少只兔子？

对，描述兔子数量的数列就是我们熟悉的斐波那契数列，很多人都是通过这个问题了解递归的吧（也许吧，也可能是 Tower of Hanoi）？

不过兔子怎么可能“永不死去”呢！那我们现在开始考虑兔子的出生率和死亡率。先从容易的来：每对兔子父母每年生四只小兔，然后死去。如果一开始有两只兔子（第 0 年），那么第 1 年会有四只兔子，第二年会有 8 只兔子……每年兔子的数量会翻一番。记第 t 年的兔子数量为 $n_t$ ，那么： $n_t=2 \cdot n_{t-1}$ ，即 $n_t = 2^t\cdot n_0$ 。很显然，如果不受限制，兔子的数量会越来越多，最终撑满这个星球，乃至整个宇宙。

假如我们考虑种群数量增长所受的限制呢？可想而知，如果种群数量越来越多，也许很多小兔子由于太过拥挤，缺少食物和空间，没有繁殖就死去。整个种群的数量就不会呈现上述无限增长的情况了。生物学家用一种叫 logistic model 的简化方式来描述这种情况下的群体增长： $n_{t+1} = (r_{born}-r_{die})\cdot(k\cdot n_t-n_t^2)/k$。 其中，$n_t$ 为这一代的种群数量，$r_{born}$ 为出生率，$r_{die}$ 为死亡率，$k$ 为承载能力。

举个例子，如果出生率为 2，死亡率为 0.4，承载力为 32，第 1 代有 20 只兔子，套用上面的模型，那么第 2 代有 12 只兔子；再把这个结果代入计算，会得出第三代仍然有 12 只兔子；从此种群数量维持在 12。

如果我们改变一些参数，比如把死亡率降到 0.1，那么依据模型计算，第 2 代有 14.25 只兔子，第三代为 15.01816 只兔子（不要在意兔子的数量为什么可以是小数）。实际上我们的计算过程是把这一代的计算结果代入模型公式，计算下一代的结果，这个重复不断的过程就是迭代，对模型进行迭代。

logistic map

由 logistic model 进行迭代计算还是有些麻烦，我们可以再进行一点简化：把出生率和死亡率合成一个变量 $R$，种群数量由承载率（当前种群数量与最大可能的种群数量的比率）$x$ 代替，$x = n / k$，由于当前种群数量总是介于 0 和 $k$ 之间，所以 $x$ 总是介于 0 和 1 之间。

那么我们就可以把上面的 logistic model 的公式改写一下，于是我们有： $x_{t+1}=R \cdot x_t \cdot (1-x_t)$。这个方程称为 logistic map，是动力系统理论和混沌研究中的一个重要方程。

如果我们让 $R$ 值变化，那么 logistic map 就很有趣了。

不妨先假定 $R=2$，我们发现，不管 $x$ 的初始值是什么（先用 0.2 试试吧），最后总会达到同一个固定的值：

不同的初始值只会让到达 0.5 的速度有快有慢，但经过若干步骤后，都会到达 0.5。那么这个 0.5 就称为不动点（fixed point）。

我们把 $R$ 的值调大，也许这样的不动点依然后存在，但到达不动点的速度会越来越慢。假如 $R=3.1$ ，我们再来看看，会发现情况似乎不太一样了：

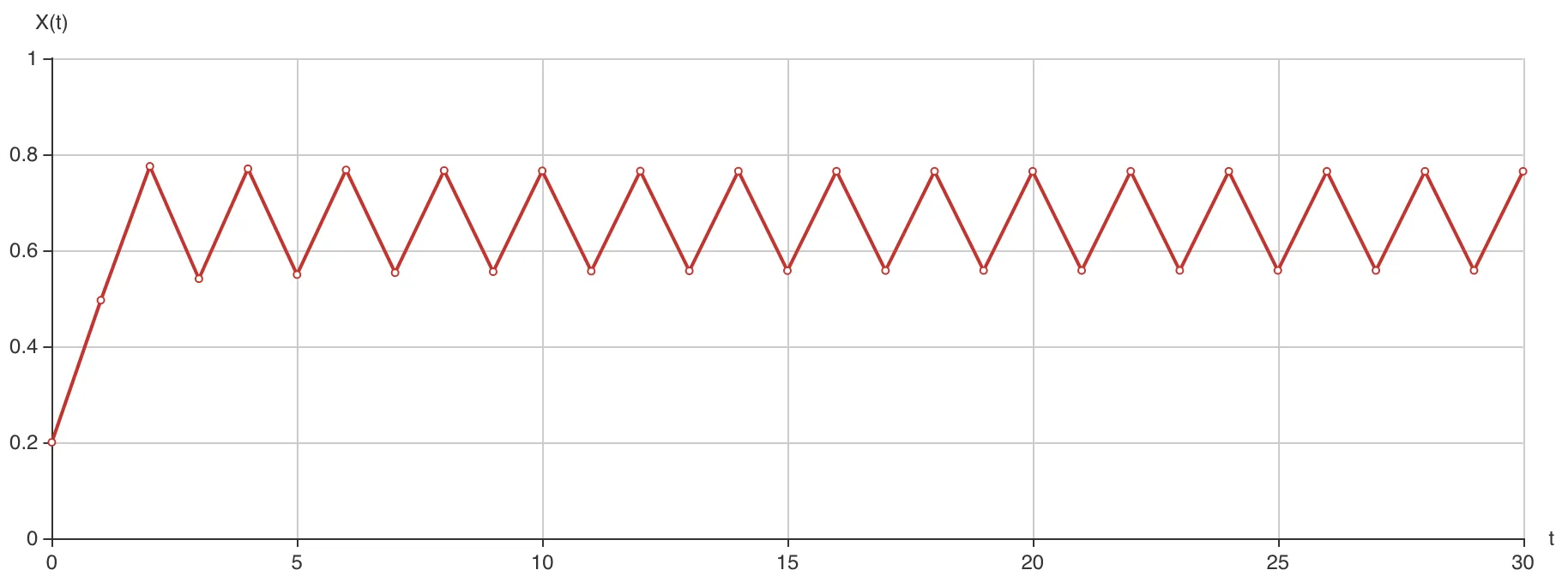
R=3.1，x₀=0.2

$x$ 的值最终会在 0.5580141 和 0.7645665 之间振荡。我们称之为吸引子。

随着 $R$ 值的变化，情形会更加复杂。我从 wikipedia 上把结论摘录如下：

1. 0 和 1 之间：不论初始值数值为何，$x$ 会越来越少，最后趋近于 0。
2. 1 和 2 之间：不论初始值数值为何，$x$ 会快速的趋近 $(R-1)/R$。
3. 2 和 3 之间：经过几次迭代，$x$ 也会越来越接近 $(R-1)/R$，但一开始会在这个值左右振动，而收敛速率是线性的。
4. 3：$x$ 仍然会越来越接近 $(R-1)/R$，但收敛速率极为缓慢，不是线性的。
5. 3 和$1+\sqrt{6}$（约 3.45）之间：针对几乎所有的初始值，$x$ 最后会在 2 个值之间持续的震荡，即 x 最后会是 a,b,a,b… 的变化，其数值和 $R$ 有关。
6. 3.45 和大约 3.54 之间，针对几乎所有的初始值，$x$ 最后会在 4 个值之间持续的震荡。
7. 约大于 3.54：$x$ 最后会在 8 个、16 个、32 个值……之间持续的震荡，至于 $R$ 何时会令 $x$ 的值由 n 个到 2n 个，则和 费根鲍姆常数 $\delta = 4.669...$ 有关。
8. 约为 3.5699：这样的振动消失，整个系统开始在 混沌 的状态之中。针对几乎所有的初始值，都不会出现固定周期的震荡，初值再微小的变化，随着时间都会使结果产生明显的差异，这就是典型混沌的特性。
9. 大于 3.5699：整个系统在 混沌 的状态之中。不过，当中有些特定的 $R$ 值还是使系统变成非混沌，有周期性的结果，这些区间称为“稳定岛”。例如当 $R$ 约大于 3.82，会出现 3 个值的周期，再大一点出现 6 个值及 12 个值的周期。
10. 当 $R$ 从大约 3.5699 到大约 3.8284 之间，系统混沌性质发展的现象有时会称为 Pomeau–Manneville 场景，其特征是周期性的震荡和非周期性的行为会穿插出现。此特征可以应用在半导体元件中。也有其他区域会使系统的周期为 5 个值，不管任意周期都存在某特定的 $R$，使周期为指定值。
11. 大于 4：针对几乎所有的初始值，系统最后都会超过区间 [0,1] 并且发散。

似乎有点枯燥，不过没关系，我们来画个图吧，通过图形来了解一下这个混沌系统。取一个超过 3.5699， 不超过 4 的 $R$ 值，这里我们不妨取 $R = 4$，还是令 $x$ 初始值是 0.2，那么迭代 100 次：

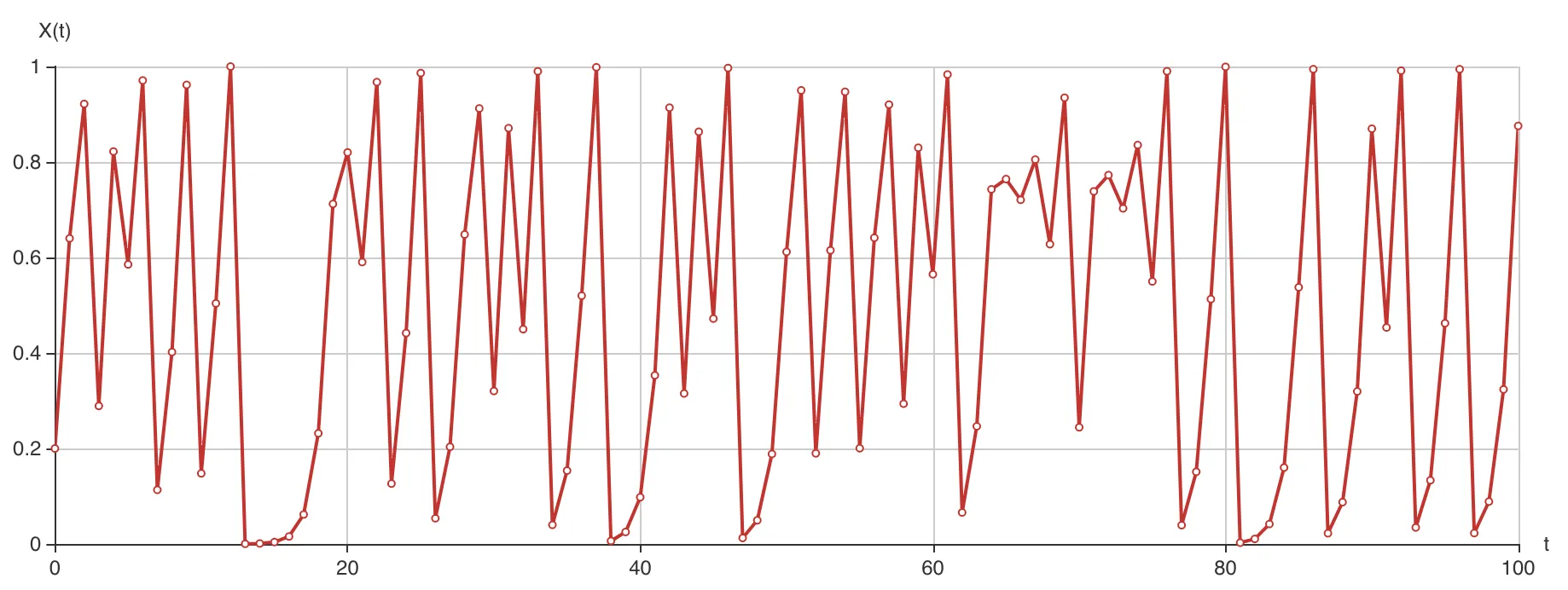
R=4，x₀=0.2

一个感觉，杂乱无章。对于每个 $x$ 的值，虽然它能唯一决定下一个 $x$ 的值是什么，但它们却组合成一个看起来非常随机的轨迹。在计算机中，我们甚至可以用它来生成伪随机数。因此，表面的随机性可能来自非常简单的确定性系统。

不仅如此，对于一个能产生混沌的 $R$ 值，如果初始值有任何的不确定性，那么一定时间后的轨迹就无法预测了。还是刚刚的图，我们考虑稍稍修改一下初始值，比如修改小数点后第 10 位，假定初始值是 0.2000000001 会怎么样？这与 0.2 非常接近，我们把两条轨迹绘制到一起看看：

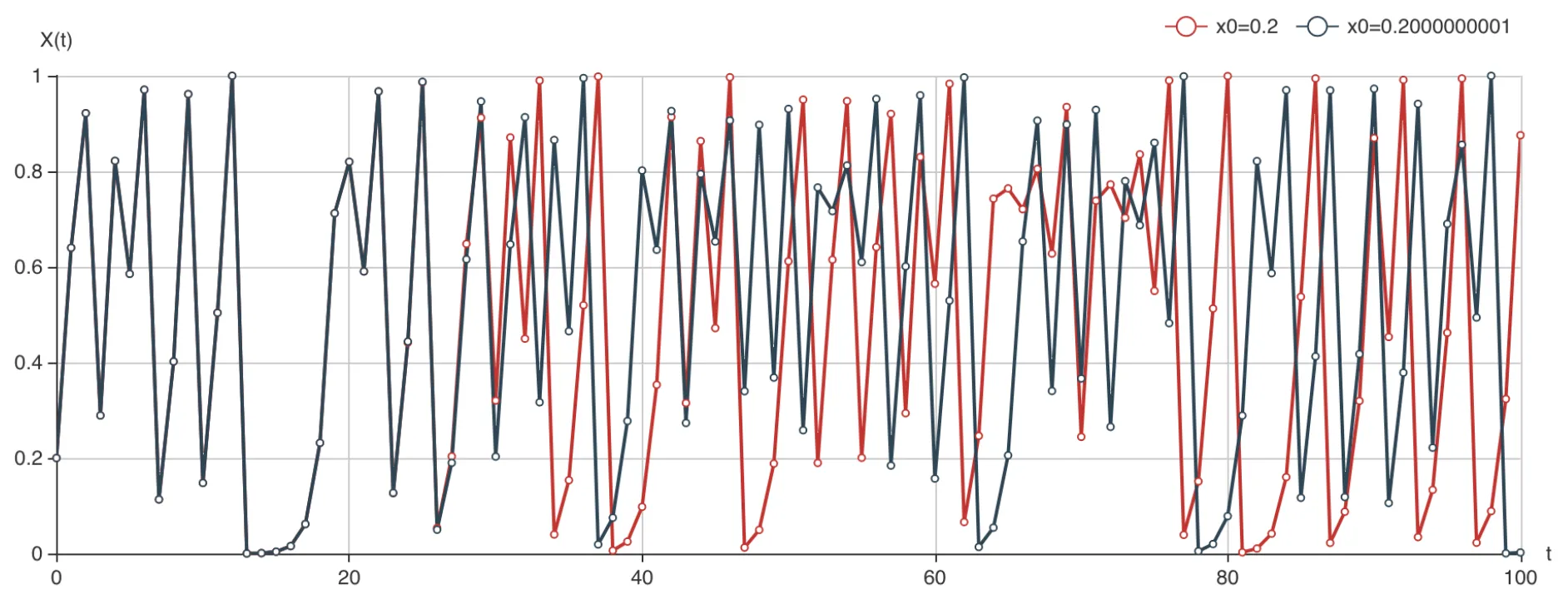
可以看出，大概在 $t = 30$时，两条轨迹已经分开，$x$ 的值已经无法预测了。实际上只要初始值有不确定性，不管精确到小数点后多少位，最终都会在 $t$ 大于某个值的时候变得无法预测。

伪随机算法

接下来，我们就来尝试使用 logistic model 的混沌特性来实现一种简单的伪随机算法。

function* RandomGenerator() {
  let seed = 0.2;
  function getNext(x) {
    return 4 * x * (1 - x);
  }
  for (let i = 0; i < 30; i++) {
    seed = getNext(seed);
  }
  while (true) {
    seed = getNext(seed);
    yield seed;
  }
}
 
const randomGenerator = RandomGenerator();
 
function random() {
  return randomGenerator.next().value;
}

实际上一些常见的伪随机数生成算法，例如线性同余法，也是使用了类似的手段，通过迭代产生混沌系统。而这类的算法所追求的，我觉得有三个方面的内容：

1. 统计意义上的随机，即随机数结果分页均匀，不能有所倾向。
2. 更大的循环区间。比如像如上算法，受 $R$ 值和计算机浮点数精度的影响，一定会在某个时刻产生与之前相同的结果，使得迭代进入循环。而用线性同余算法，循环区间则与选取的模数大小相关。
3. 更快的性能。